ADMM for Generalized Lasso Inference

Sparsity plays an important role in machine learning, statistics, and signal processing. In the basic set up, we are given a noisy observation \(y\in\mathbb{R}^m\) and a dictionary \(D \in \mathbb{R}^{m\times n}\). The goal is to estimate the weights \(w \in \mathbb{R}^n\) that produce the observation under the assumption that most of its entries have a value of zero. A popular approach to obtaining sparse solutions is through the class of \(\ell_1\) penalized regression problems. Mathematically, these are written as

where \(F \in \mathbb{R}^{k \times n}\) encodes \(K\) distinct \(\ell_1\)-norm penalties, and \(\lambda \geq 0\) is a lagrange multiplier that determines the strength of those penalty terms. In statistics, this is also known as the generalized Lasso problem [1]. The main challenge with solving equation \(\ref{eq:general-lasso}\) lies in the non-differentiability of the \(\ell_1\)-norm. Therefore, we cannot obtain an analytical solution and must resort to iterative solvers.

Deriving an ADMM algorithm

An overview of the ADMM framework can be found here . We can rewrite the generalized Lasso into ADMM form by introducing a variable \(z\) and a constraint which transforms equation \(\ref{eq:general-lasso}\) into the following problem

The corresponding scaled Augmented Lagragian is given by

Note that introducing \(z\) doesn’t change the optimal solution since the additional penalty terms in \(L\) are minimized when \(w-z=0\). However, we benefit from separating the \(\ell_1\) penalty from the reconstruction term. ADMM proceeds with block minimization under \(L\). This consists of an \(w\)-minimization step, a \(z\)-minimization step, and a gradient ascent update step on the dual variables \(u\).

Updating \(w\)

The standard ADMM update for \(w\) is given by

To obtain the RHS, we set the partial derivative of equation \(\ref{eq:L}\) wrt. \(w\) to zero.

Now rearrange to collect terms with \(w\) on the LHS and all other terms on the RHS.

Factorize and solve for \(w\).

\(w^*\) minimizes the augmented Lagrangian given our previous estimates of \(z_k\) and \(u_k\) and becomes the closed-form update rule for \(w_{k+1}\).

Updating \(z\)

Next, we find the ADMM update for \(z\)

Similarly, we set the partial derivative of \(L\) wrt. \(z\) to zero

Immediately, we encounter the non-differentiable \(\ell_1\) term. We can proceed by observing two facts. 1) The overall \(\ell_1\) penalty can be decomposed as a sum of \(\ell_1\) separate penalties placed on each component of \(z\), i.e. \(\|z\|_1 = \sum_{i=1}^N |z_i|\). Therefore, we can deal with each component independently. And 2) For each component, there exists only a single discontinuity centered around zero, and that the derivative exists for all other values. Therefore, we can split this problem into two cases \(z=0\) and \(z\neq 0\).

For \(z \neq 0\), the derivative is equal to the \({\rm sign} (z)\) which can be substituted into equation \(\ref{eq:L_z}\) to get

Collecting all terms with \(z\) on the LHS and all others on the RHS, we get

When \(z < 0\), then \(Fw + u < -\frac{\lambda}{\rho}\) and when \(z > 0\), then \(Fw + u > \frac{\lambda}{\rho}\). This observation can be compactly written as \(|Fw + u| > \frac{\lambda}{\rho}\) and \({\rm sign}(z) = {\rm sign}(Fw+u)\) to get the update

When \(z = 0\), we must deal with the discontinuity using subgradients, which is given by \(\partial \| z\|_1 =[-1,1]\). The optimality condition is zero exists within the subgradient. Substituting this into equation \(\ref{eq:L_z}\),

which can be rearranged to get the form

In words, \(z=0\) is an optimal solution only when \(Fw+u\) is within the region \(\left[-\frac{\lambda}{\rho},\frac{\lambda}{\rho}\right]\). Combining the results above for \(z \neq 0\) with \(z = 0\), we get the following updates

More compactly this can be written using the soft-threshold operator \(\mathcal{S}\). The update equation for \(z\) is given by

Updating \(u\)

Given the updated \(w_{k+1}\) and \(z_{k+1}\), we perform a gradient ascent update to the dual variables. This is simply given by the running sum of residuals

Special Cases of the Generalized Lasso

For different choices of \(F\), we recover several well-studied problems as special cases.

Standard Lasso

When \(F\) is an identity matrix \(I\in\mathbb{R}^{n \times n}\), we recover the standard Lasso problem [2]

This model is commonly used in compressed sensing where we are interested in sparse signal recovery, and can be used as a convex relaxation for \(\ell_0\)-norm variable selection problem .

Variable Fusion

When \(F \in \mathbb{R}^{(n-1) \times n}\) is a first order difference matrix,

we obtain the variable fusion model [3] which corresponds to the problem

This model is used when we expect the ordering of the weights to have smooth structure.

Fused Lasso

When \(F \in \mathbb{R}^{(2n-1)\times n}\) combines both the penalty from the standard lasso and the variable fusion,

we obtain the Fused Lasso model [4] which combines both a sparsity and smoothness penalty.

Demo

I illustrate the impact of the various penalties mentioned earlier on the inference results. Noisy observations are generated from a random dictionary using smooth and sparse weights. For a given set of hyperparameters, we obtain the following ADMM solutions

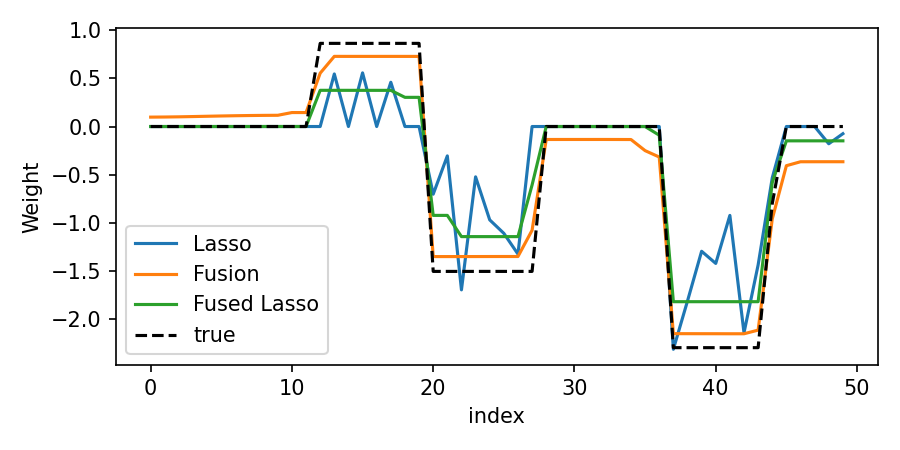
The standard lasso problem encourages shrinkage towards zero of each weight independently. While it accurately captures certain regions with active support, adjacent weights can have large variance. On the other hand, the variable fusion model prioritizes smooth patterns and effectively identifies distinct areas of smoothness. However, since its penalty does not promote zero shrinkage, it incorrectly identifies that the entire support is active. The fused Lasso model excels in accurately identifying both smoothness and the active support set. Importantly, note that solutions across all models exhibit a bias towards lower magnitudes than the actual weights. This is because \(\ell_1\) inference provides a biased estimate of the weight vector.

Code

This experiment can be replicated with the code below and is also available here

import numpy as np
import numpy.random as npr

def soft_threshold(x, thresh):
    return np.sign(x)* np.max([np.abs(x)-thresh, np.zeros(len(x))], axis=0)

def ADMM_generalized_lasso(y, D, F, rho, lam, n_iters=100):

    # y: (m,) array. observation 

    # D: (m, n) array. dictionary

    # F: (k, n) array. constraint matrix

    # rho: augmented lagrange multiplier

    # lam: lagrange multiplier


    n = len(D.T)

    # random initialization

    w = npr.randn(n) 
    u = npr.randn(len(F)) 
    z = npr.randn(len(F)) 
    
    FtF = F.T @ F

    for i in range(n_iters):
        w = np.linalg.lstsq(D.T @ D + rho * FtF, D.T @ y + rho * F.T @ (z-u), rcond=None)[0]
        z = soft_threshold(F @ w + u, lam/rho)
        u = u + F @ w - z
        
    return w

from sklearn.datasets import make_sparse_coded_signal
import matplotlib.pyplot as plt

n, m = 50, 100
n_nonzero_coefs = 10

# generate dictionary

_, D, _ = make_sparse_coded_signal(
    n_samples=1,
    n_components=n,
    n_features=m,
    n_nonzero_coefs=n_nonzero_coefs,
    random_state=1,
)
D = D.T



# generate structured coefficients

np.random.seed(1)
w_true = np.zeros(n)
for i in range(5):
    ix = np.random.choice(n)
    length = np.random.randint(5,10)
    w_true[ix:ix+length] = npr.randn()
    
    
# generate noisy observations 

y_true = D @ w_true
y = y_true + npr.randn(m)*0.2


# define hyperparameters

rho = 0.3 # augmentation multiplier

lam = 0.5 # general multiplier for L1

lam2 = 0.3 # multipler for sparsity in Fused Lasso




# construct F matrices

F_Lasso = np.eye(n) # Lasso solution

F_fusion = (np.diag(np.ones(n),k=1)[:-1,:-1] + np.diag(np.ones(n)*-1,k=0))[:-1] # Fusion Penalty solution

F_fusedLasso = np.concatenate([np.diag(np.ones(n)/lam*lam2), F_fusion]) # Fused Lasso solution


# compute ADMM solution

w_lasso = ADMM_generalized_lasso(y, D, F_Lasso, rho, lam)
w_fusion = ADMM_generalized_lasso(y, D, F_fusion, rho, lam)
w_fusedLasso = ADMM_generalized_lasso(y, D, F_fusedLasso, rho, lam)


    
# Plot

plt.figure(figsize=(6,3))
plt.plot(w_lasso, label="Lasso")
plt.plot(w_fusion, label="Fusion")
plt.plot(w_fusedLasso, label="Fused Lasso")
plt.plot(w_true, 'k--', label="true")
plt.ylabel("Weight")
plt.xlabel("index")
plt.legend()
plt.show()
    

1. Ryan J Tibshirani. “The solution path of the generalized lasso”. 2011.
2. Robert Tibshirani. “Regression shrinkage and selection via the lasso”. Journal of the Royal Statistical Society Series B: Statistical Methodology, 1996.
3. S Land, and J Friedman. “Variable fusion: a new method of adaptive signal regression”. Technical Report, Department of Statistics, Stanford University, 1996.
4. Robert Tibshirani, Michael Saunders, Saharon Rosset, Ji Zhu, and Keith Knight. “Sparsity and smoothness via the fused lasso”. Journal of the Royal Statistical Society Series B: Statistical Methodology, 2005.